100+ Data Interpretation Bar Graph Questions and Answers - 1

Study the following graph carefully and answer the questions given below:

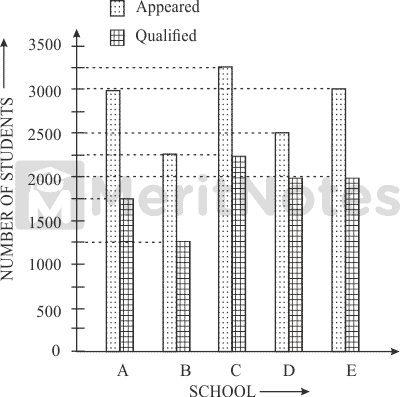
Question: 1

Total number of Students Appeared and qualified from various Schools at a Scholarship Exam.
The average number of students qualified in the examination from Schools C and D is what percent of the average number of students appeared for the examination from the same schools?

(A) 58.62

(B) 58.96

(D) 73.91

View Answer

Ans: D

Average number of students qualified from C and D

= $${1}/{2}(2250 + 2000)$$ = $${4250} / {2}$$ = 2125.

Average number of students appeared from C and D

= $${1}/{2}(3250 + 2500)$$ = $${5750}/{2}$$ = 2875.

Required% = $$({2125} / {2875} × 100)$$% = $$({85}/{115} × 100)%$$ = $${1700}/{23}$$ = 73.91%.

Question: 2

What is the ratio of the numbers of students appeared to the number of students qualified at the scholarship exam from School C?

(A) 6 : 5

(B) 7 : 12

(D) 13 : 9

View Answer

Ans: D

(Number of students appeared from C) : (Number of students qualified from C)

= $${3250}/{2250}$$ = $${13} / {9}$$ = 13 : 9.

Question: 3

What is the ratio of the number of students qualified in the scholarship examination from School A and the number of students qualified in the examination from School B?

(A) 7 : 3

(B) 7 : 5

(D) 8 : 5

View Answer

Ans: B

(Number of students qualified from A) : (Number of students qualified from B)

= $${1750} / {1250}$$ = $${7}/{5}$$ = 7 : 5.

Question: 4

The number of students appeared for the scholarship exam from School D is approximately what percent of the total number of students appeared for the exam from all the schools together?

(A) 12

(B) 18

(D) 48

View Answer

Ans: B

Required %

= $$[{2500} / {(3000 + 2250 + 3250 + 2500 + 3000)} × 100]%$$

= $$({2500} / {14000} × 100)$$%

= $${125}/{7}$$% = 18%(nearly).

Question: 5

What is the difference between the average number of students appeared in the scholarship exam from all the given schools and the average number of students qualified from all the schools together?

(A) 950

(B) 990

(D) 1100

View Answer

Ans: A

Average number of students appeared from all the schools = $${1}/{5}(3000 + 2250 + 3250 + 2500 + 3000)$$ = $${14000} / {5}$$ = 2800.

Average number of students qualified from all the schools = $${1}/{5}(1750 + 1250 + 2250 + 2000 + 2000)$$ = $${9250}/{5}$$ = 1850.

Required difference = (2800 - 1850) = 950.

Model MCQ Online Test

Error Report!

100+ Data Interpretation Bar Graph Questions and Answers - 1

REGISTER TO GET FREE UPDATES