100+ Data Interpretation Pie Chart Questions and Answers - 1

Study the Pie chart carefully and answer the questions:

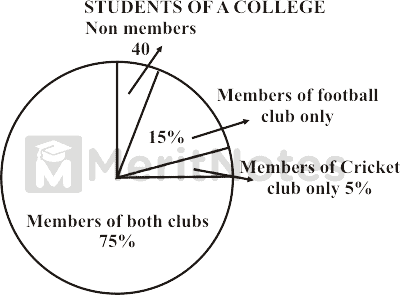
Question: 1

Percentage of students who are not members of any club is

(A) 2%

(B) 5%

(D) 9%

Ans: B

Percentage of students who are members of any club = 75 + 15 + 5 = 95%.

Percentage of students who are not members of any club = 100 – 95% = 5%.

Question: 2

Number of students who are members of cricket club only

(A) 30

(B) 35

(D) 45

Ans: C

Number of students who are not members of any club = 40 = 5%.

Percentage of members of cricket cub only = 5%.

Number of members of cricket club only = 40.

Question: 3

Ratio of members of cricket club only and football club only respectively is

(A) 1 : 2

(B) 1 : 3

(D) 2 : 3

Ans: B

Percentage of member of cricket club only = 5%.

Percentage of member of football club only = 15%.

Required ratio = 5 : 15 = 1 : 3.

Question: 4

The number of students who are members of both the club is

(A) 500

(B) 550

(D) 650

Ans: C

Let total number of students of a college be x.

Non members students = 40

∴ $$ {x × 5} / {100}$$ = 40

X = $${100 × 40} / {5}$$ = 800

Percentage of members of both club = 75%

Number of members of both club = $${75 × 800} / {100}$$ = 75 x 8 = 600.

Model MCQ Online Test

Error Report!

REGISTER TO GET FREE UPDATES